Salt budget and salt composition for the Aral Sea

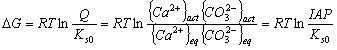
Contact person: Sergey Konovalov

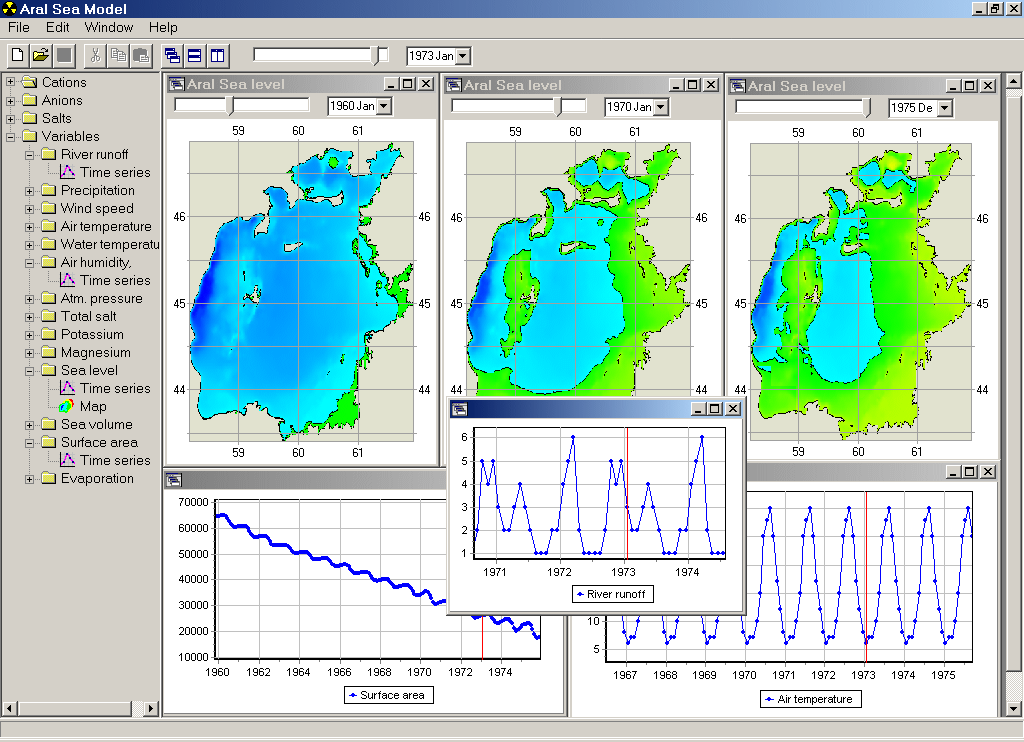
The Aral Sea looks to be the second in the row of dead seas after the Dead Sea. The sea has experienced a real ecological collapse over the last 30 years. It has progressively changed from the very productive marine system, which provided various marine resources and recreational potential, to a highly polluted shrinking water body that is a source of contaminants for surrounding areas. The volume of water of the Aral Sea progressively decreases and, in particular, salinity has already increased from about 10 - 11 to more than 30 - 40. It approaches the stage, when salinity becomes non-conservative, as individual salts reach the limit of solubility and actively precipitate. This work is aimed to investigate possible changes in the salt budget and composition applying a "0"-D model of dissolution and precipitation of minerals.

In a general way, for an electrolyte that dissolves in water according to the reaction Cat_mAn_n(s) ↔ mCat⁺ⁿ(aq) + nAn^-m(aq) the equilibrium condition can be represented by {Cat_mAn_n(s)} = {Cat⁺ⁿ(aq)}^m ·{An^-m(aq)}ⁿ and the conventional solubility expression K_s0= {Cat⁺ⁿ(aq)}^m ·{An^-m(aq)}ⁿ. In order to estimate precipitation and dissolution of a salt, there is a need to characterize the solubility of this salt as a function of the concentration/activity of cation and anion from the respective solubility product (K_so). The solubility equilibrium is influenced by the ionic strength of the solution and temperature. In order to test whether seawater is over- or undersaturated, we inquire whether the free energy of dissolution of the solid phase is positive, negative, or zero; that is, for the solubility equilibrium of calcite (CaCO_3(S) = Ca²⁺ + CO₃^2- K_s0) the free energy of dissolution is given by

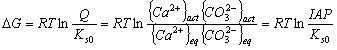
The actual ion activity product, IAP, may be compared to K_s0. The state of saturation of a solution with respect to a solid is defined as follows: (oversaturated), (equilibrium, saturated), and (undersaturated).

We considered the next solid phases:

No	Salt Composition	IAP	Ks0
1			8.13E-18
2			3.52E-09
3			3.47E-08
4			2.24E-4
5			0.93
6			1.23
7			7.00
8			8.45
9			8.98
10			16.80
11			27.12
12			30.19
13			457.71
14			621.68
15			801.6

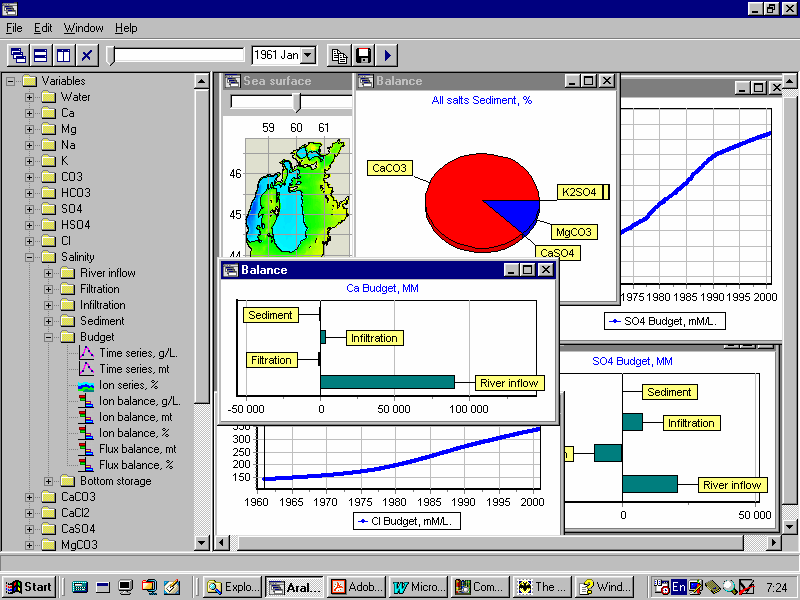
While the upper three components control precipitation of minerals in the ðcarbonate oceanõ, and the middle components control precipitation in the ðsulfate oceanõ, the last 6 components control the ðchloride oceanõ, when precipitation of minerals affects the water budget and can result in a complete mineralization of the system.

To calculate coefficients of activity for every considering ion (Ca²⁺, Mg²⁺, Na⁺, K⁺, SO₄^2-, HSO₄^-, HCO₃^-, CO₃^2-, Cl^-) for an individual temperature and salinity, we have used the next equation:

As natural systems are never fully equilibrated, we have applied a kinetic method and considered that solid salts can precipitate or dissolve at every step of integration. The inventory of every solid salt at the bottom of the sea is considered to be exponentially decreasing implementing a natural burial process. Solid salts at the dried shore are parameterized to be lost from the system (irreversibly buried), though the shore might be flooded lately.

We have assumed that the system approaches equilibrium conditions at every step of integration. We compare the above calculated IAP values to the conventional solubility product to estimate the state (oversaturation/undersaturation) of the considered salts. The mass of a solid salt that is precipitated/dissolved at every step depends on over-/undersaturation, the total mass of the individual salt in water and a specific rate of the process:

,

where F is normalized over-/under-saturation, and M is the maximum (moles/liter) of an individual salt that can precipitate or dissolve.

Results of numerical experiments suggest different scenarios of volumetric and morphometric changes for the Aral Sea and variations in the salt budget and composition depending on the water budget and the load of cations and anions to the sea.